Polígono Spin: Classificação de Polígonos

A classificação de polígonos é feita em relação ao número de lados da forma poligonal.

Um polígono é uma forma geométrica fechada que é constituída por segmentos de reta que não se cruzam. A depender da quantidade de segmentos que formam esse polígono, ele diferenciar-se-á dos outros. Por essa razão, a classificação de polígonos é feita em função do número de lados. Vamos observar as formas a seguir:

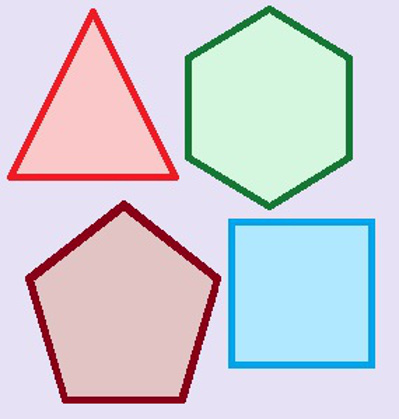
Todas essas figuras são polígonos, mas não são iguais, diferenciam-se pela quantidade de lados de cada um

Essas formas poligonais acima se diferenciam pela quantidade de lados, isto é, pela quantidade de segmentos de reta que as formam. A figura vermelha é formada por três segmentos de reta, logo, possui três lados. A forma verde possui seis lados; a forma marrom, cinco; e a forma azul possui quatro lados. Mas se essas cores forem alteradas, haverá

mudança na forma geométrica desenhada? Não! Então, precisamos de uma maneira mais eficiente para nomear essas figuras. Essa maneira eficiente existe, e nós podemos classificar essas figuras de acordo com o seu número de lados. Para formar o nome de cada figura, precisamos comentar um pouco sobre a língua grega, pois utilizamos prefixos originários dela. Esses prefixos gregos fazem referência exatamente a números, são eles:

3 – tri	8 – octa	13 – trideca	18 – octadeca
4 – tetra	9 – enea	14 – tetradeca	19 – eneadeca
5 – penta	10 – deca	15 – pentadeca	20 – icosa
6 – hexa	11 – hendeca	16 – hexadeca
7 – hepta	12 – dodeca	17 – heptadeca

Já que estamos falando sobre prefixos gregos, vale a pena lembrar que o nome polígonos também possui origem grega, significando poly (muitos) gon (ângulos). Mas por que ângulos, se estamos falando de lados? Um ângulo é formado pelo encontro de duas retas ou também de dois segmentos de retas, logo, se aumentamos a quantidade de segmentos de retas da figura, estamos aumentando a quantidade de ângulos. Olhe novamente a imagem acima, observe que a figura vermelha tem três lados e três ângulos; a figura azul tem quatro lados e quatro ângulos e assim sucessivamente. Podemos concluir que, para cada polígono, a quantidade de ângulos e de lados é a mesma!

Não pare agora... Tem mais depois da publicidade ;)

Então, para realizarmos a classificação de polígonos, utilizamos o prefixo grego que corresponde a sua quantidade de lados, unindo-o ao sufixo gono ou látero (lados). Apenas para algumas figuras haverá uma pequena diferença na escrita, isso ocorre apenas para que a pronúncia do nome seja mais agradável. Logo a seguir esses nomes estarão sublinhados.

Portanto, em relação ao número de lados, os polígonos podem receber os seguintes nomes:

3 lados → triângulo ou trilátero

4 lados → quadrângulo ou quadrilátero

5 lados → pentágono ou pentalátero

6 lados → hexágono ou hexalátero

7 lados → heptágono ou heptalátero

8 lados → octágono ou octalátero

9 lados → eneágono ou enelátero

10 lados → decágono ou decalátero

11 lados → undecágono ou undecalátero

12 lados → dodecágono ou dodecalátero

15 lados → pentadecágono ou pentadecalátero

20 lados → icoságono ou icolátero

Agora que já aprendemos a realizar a classificação de polígonos, podemos nomear as figuras de nossa ilustração como:

Forma poligonal vermelha: Triângulo

Forma poligonal verde: hexágono

Forma poligonal marrom: pentágono

Forma poligonal azul: quadrilátero

Aproveite para conferir nossa videoaula sobre o assunto:

Os polígonos podem ser classificados em relação ao número de lados

Por: Amanda Gonçalves Ribeiro

ARTIGOS RELACIONADOS

Tangram

O que é Tangram, como surgiu o Tangram, características do Tangram, o Tangram e o desenvolvimento da criatividade.

Área do trapézio

Você sabe o que é um trapézio? Clique e aprenda a calcular área do trapézio!

Propriedades do Paralelogramo

Relacionando as características de um paralelogramo.

Soma dos ângulos internos de um polígono convexo

Fórmula para o cálculo da soma dos ângulos internos de um polígono

Números figurados

Você sabe o que são os números figurados? Clique aqui e confira!

Congruência de figuras geométricas

Aprenda como definir a congruência de figuras geométricas planas analisando exemplos comentados.

Polígonos semelhantes

Veja alguns casos de polígonos semelhantes e algumas propriedades decorrentes da semelhança entre eles.

Quadriláteros

Clique e aprenda o que são quadriláteros e o modo como essas figuras que possuem quatro lados são classificadas.

Ângulos

Clique para aprender o que são ângulos, como medi-los da maneira correta, para que serve um transferidor e alguns dos ângulos mais importantes.

Poliedros

Clique para descobrir o que são poliedros, as definições básicas dos poliedros mais importantes e algumas classificações desses sólidos geométricos.

Área do prisma

Clique para aprender a calcular a área de um prisma a partir da soma das áreas de todas as suas faces.

Área do polígono regular

Clique e descubra como calcular a área de um polígono regular e aprenda como sua fórmula pode ser demonstrada.

Polígonos regulares

Clique e descubra o que são polígonos regulares, obtenha exemplos e aprenda suas principais propriedades envolvendo as medidas de seus ângulos.

Polígonos convexos

Clique e aprenda o que são polígonos convexos, quais seus elementos mais importantes e suas propriedades mais usadas e conhecidas.

Trapézio

Aprenda o que é um trapézio, e veja quais são os tipos existentes. Saiba como calcular seu perímetro e sua área por meio de fórmulas e observando os exemplos.